2.2 Monopôle vertical court
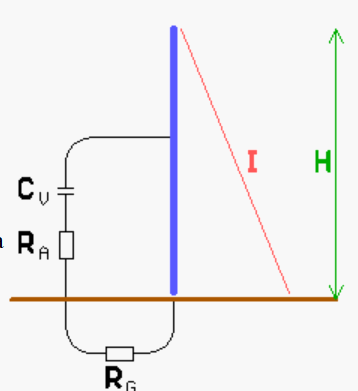 Supposons que nous ayons un monopôle vertical court d'une hauteur H et alimenté par rapport au sol . Si H est faible par rapport à la longueur d'onde alors :
Supposons que nous ayons un monopôle vertical court d'une hauteur H et alimenté par rapport au sol . Si H est faible par rapport à la longueur d'onde alors :
• L'antenne agira en tant qu'une capacité (CV) en série avec la résistance de rayonnement (RA) et la résistance de perte (RG)
• Le courant d'antenne (I) diminuera linéairement à partir du point d'alimentation vers le haut de l'antenne, où il atteindra 0
• La tension sera la même sur l'ensemble de l'antenne
La répartition actuelle, qui est différente de la distribution sinusoïdale à laquelle nous sommes habitués, peut être expliquée comme suit :
la capacité de l'antenne ne se trouve pas en un seul point sur l'antenne, mais est répartie de façon égale sur l'antenne. Quand le courant d'antenne parcourt l'antenne il "disparaît" graduellement au travers de cette capacité répartie, ce qui entraîne une diminution linéaire.
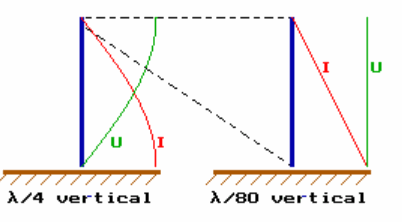 Une autre façon de voir les choses - et peut-être plus correcte - est de comparer un monopôle vertical court avec un quart d'onde verticale fullsize. Le quart d'onde fullsize possède un courant sinusoïdal et distribution de tension avec une phase de 90 degrés entre U et I.
Une autre façon de voir les choses - et peut-être plus correcte - est de comparer un monopôle vertical court avec un quart d'onde verticale fullsize. Le quart d'onde fullsize possède un courant sinusoïdal et distribution de tension avec une phase de 90 degrés entre U et I.
Le monopôle vertical court peut être vu comme la fin d'un quart d'onde fullsize, où la distribution de la tension est (presque) constante et la diminutions de distribution de courant est (presque) linéaire.
La résistance de rayonnement d'un monopôle vertical court avec une hauteur H et à une la longueur d'onde λ est la suivante:
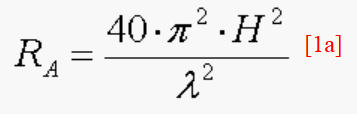
Ce qui donne à 136 kHz :
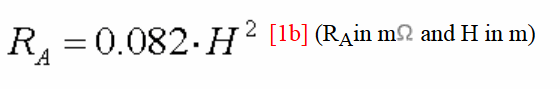
La capacité d'un brin vertical dune hauter H et d'un diamètre d est :
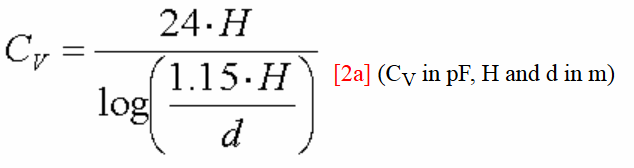
Dans la majorité des cas la formule simplifiée Cv = 6pF/m [2b] est suffisement précise
Afin d'obtenir un maximum de puissance rayonnée nous avons besoin d'un courant maximal à travers l'antenne. Cela peut être fait en compensant la composante capacitive avec un composant inductif (bobine de charge), ou autrement dit: amener l'antenne à la résonance.
En se basant sur la formule de résonance (formule de Thomson(*), nous pouvons calculer l'inductance dont nous avons besoin (voir le chapitre "bobine de charge» pour
plus détails).
Exemple :
Supposons que nous avons un long fil 10m vertical (3 mm de diamètre) avec et une perte enviromentale de 60Ω.
Sur la base de la formule [1a] le calcul de la résistance de rayonnement donne 8.2mΩ, la capacité de l'antenne, sur la base de formule [2a] est de 67pF. Pour amener l'antenne à la résonance sur 137kHz, nous aurons besoin d'une bobine de charge de 20.2mH. La réactance de la bobine est 17.4kΩ, donc si nous assumons un Q de 300 la perte de la bobine sera 58Ω . Cela porte la résistance totale de perte à 118Ω (60Ω + 58Ω).
Si nous mettons une puissance de 100W à l'antenne, nous aurons un courant d'antenne de 0.92A, la puissance rayonnée résultante sera de 6.95mW et une tension de 16 kV aux bornes de la bobine de charge.67
Dans l'exemple ci-dessus, nous avons calculé une puissance rayonnée de 6.95mW (0.92A dans 8.2mΩ). Pour obtenir l'ERP (puissance apparente rayonnée)
nous devons prendre en compte le gain de l'antenne, pour un monopôle vertical court c'est 2.6dBd. Ainsi, la puissance calculée dans ce cas sera 12.6mW ERP.
(*) Développement des calculs :
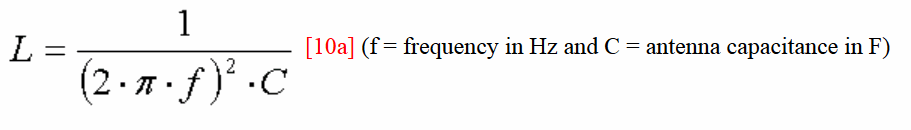
à 137 kHz L = 20.16 mH
Reactance : XL = 2ΠfL = 6.28*137000*.00202=1737.9Ω(1740Ω)
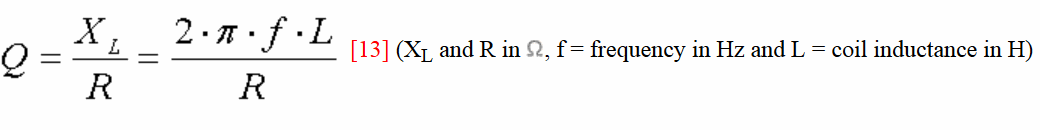
R = 2ΠFL/Q = 6.28*137000*0.0202/300 = 57.9Ω(58Ω)
Retour à la table des matières
Traduction de l'article de ON7YD http://www.on7yd.strobbe.eu/136ant/